运算放大器 —— 快速复苏笔记[贰]（应用篇）

[lab.magiconch.com][福音戰士標題生成器]-1727599199035 标准监督

阅读前请参考专栏前一篇文章，了解一些基础知识。

资源获取

写这篇文章的原因是我经常会忘记运放是如何使用的，希望通过几个样例和分析能快速且详细的分析出来。部分电路的仿真和电路仿真软件，我已经上传到云盘，这里推荐阿里的云盘，不限速下载很快，下载地址。提取码: 00kx。

前置知识

基尔霍夫定律

基尔霍夫电流定律也叫KCL。是说电路中任一节点上所流入的电流等于所流出的电流，也就是节点上电流的代数合为0。

jehf

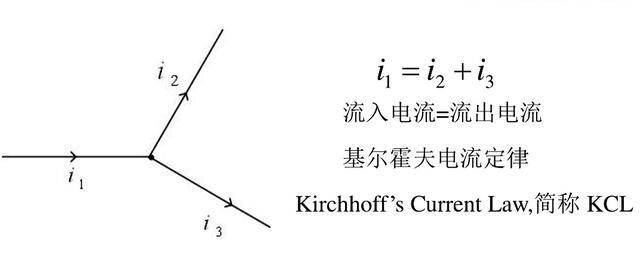
节点:一个电路的分支点。在这里，可以把任意封闭曲线或曲面，看作一个广义的节点。像力学上的质量一样，可以把物体抽象成质点来分析。

img

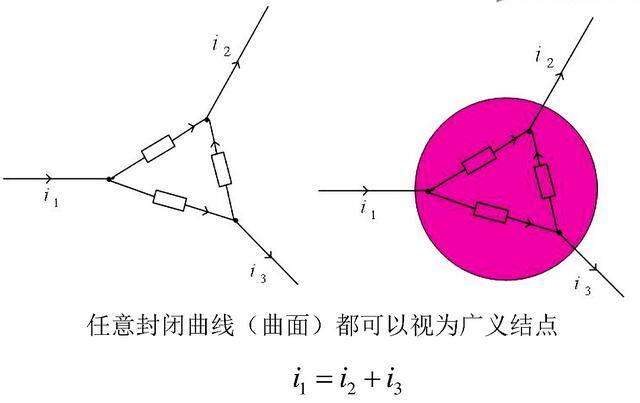
简单来说你可以直接画一个圆，对于这个圆来说，这个圆就是一个节点，进入和出去这个圆的电流合为0。

齐纳二极管/稳压二极管/Zener diode

稳压二极管的特点就是击穿后，其两端的电压基本保持不变。这个电压在手册中常说的是Nominal Zener Voltage，标称稳压值。这样，当把稳压管接入电路以后，若由于电源电压发生波动，或其它原因造成电路中各点电压变动时，负载两端的电压将基本保持不变。

其反向特性是在反向电压低于反向击穿电压时，反向电阻很大，反向漏电流极小。但是，当反向电压临近反向电压的临界值时，反向电流骤然增大，称为击穿，在这一临界击穿点上，反向电阻骤然降至很小值。尽管电流在很大的范围内变化，而二极管两端的电压却基本上稳定在击穿电压附近，从而实现了二极管的稳压功能。其原理的关键点就在于过了稳压值的时候电阻很小，即使加上不同的电压，流过的电流也不会让其两端电压变化很大，这就达到了稳压的效果。

v2-5bbc8b3d2670ef1ebc2e4906359962df_720w

主要参数

稳定电压(Uz)

指稳压二极管通过额定电流时两端产生的稳定电压值。该值随工作电流和温度的不同而略有改变。由于制造工艺的差别，同一型号稳压二极管的稳压值也不完全一致。例如，2CW51型稳压二极管的Vzmin为3.0V, Vzmax则为3.6V。

额定电流(Iz)

指稳压二极管产生稳定电压时通过该管的电流值。低于此值时，稳压二极管虽并非不能稳压，但稳压效果会变差;高于此值时，只要不超过额定功率损耗，也是允许的，而且稳压性能会好一些，但要多消耗电能。

动态电阻(Rz)

指稳压二极管两端电压变化与电流变化的比值。该比值随工作电流的不同而改变，一般是工作电流愈大，动态电阻则愈小。例如，2CW7C稳压二极管的工作电流为 5mA时，Rz为18Ω;工作电流为1OmA时，Rz为8Ω;为20mA时，Rz为2Ω ; > 20mA则基本维持此数值。

额定功耗(Pz)

由芯片允许温升决定，其数值为稳定电压Vz和允许最大电流Izm的乘积。例如2CW51稳压二极管的Vz为3V，Izm为20mA，则该管的Pz为60mWo。

反向漏电流(IR)

指稳压二极管在规定的反向电压下产生的漏电流。例如2CW58稳压二极管的VR=1V时，IR=O.1uA;在VR=6V时，IR=10uA。

运算放大器应用

前提：

  • 虚短：

$$
Vin_+ = Vin_-
$$

  • 虚断：

$$
Iin_+ = Iin_- = 0
$$

应用1

反相比例运算电路

这里我们先把电路放上来，在看这一篇之前请先去看参数篇，运放的基础知识。详见专栏：

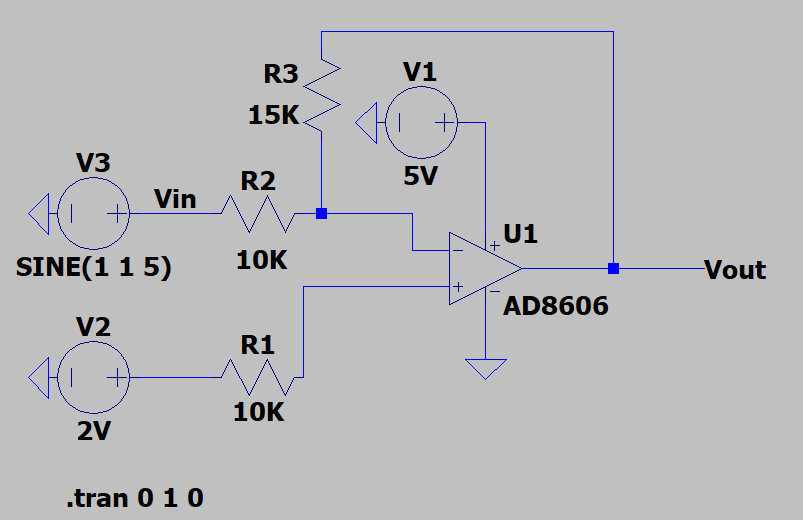
image-20220713225253744

V1是放大器电源输出为+5V的DC电压。

V2是虚拟地电压，用来模拟没有直接接地的情况。这里提供的是一个2V的DC电压

V3是正弦波，其参数如下：

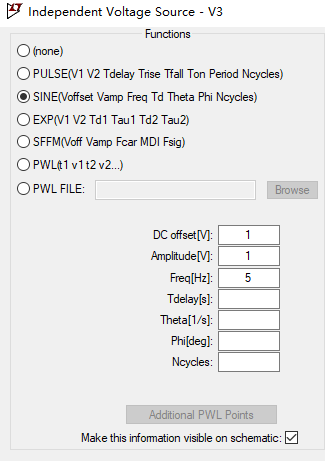
image-20220713225458473

反向放大推导：

虚短：
$$
V_+ = V_- = V_{GND}\
V_{GND}为V-和V+的值
$$
虚断：以反相输入端为节点分析。
$$
\frac{V_{in} - V_{GND}}{R_2}= \frac{V_{GND} - V_{out}}{R3}\
KCL方法推导电流相等、方向相反，以V_{GND}到V_{out}为正方向。
$$

化简得：
$$
V_{out} = V_{GND}(1+\frac{R_3}{R_2}) - V_{in}\frac{R_3}{R_2}
$$
我们试一试推导带入，上文情况下，Vout的输出结果是怎么样的：
$$
V_{out} = V_{GND}(1+\frac{R_3}{R_2}) - V_{in}\frac{R_3}{R_2}=2*(1+1.5) - V_{in}*1.5\
其中V_{in}=[0,2]，且为\sin{x}波形\
结果如下：V_{out}=[2,5]
$$
仿真的结果如下：

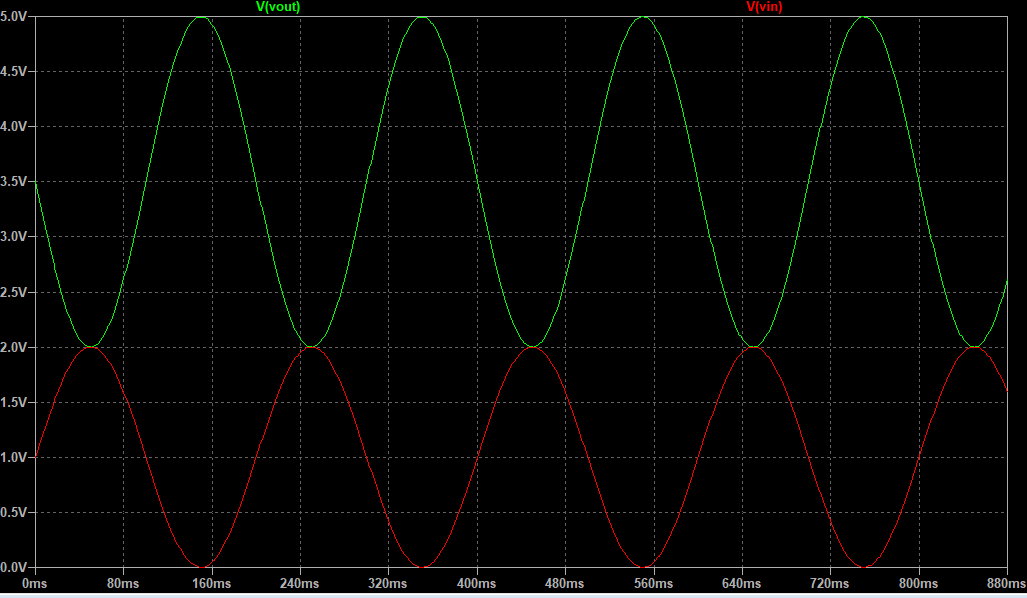
image-20220713231510637

反向放大的特殊情况

可以看到下图中我们放大器的输入+接的是GND，这是一种特殊情况，对应的输入+接的是GND就是电压为0，我们再用上文的分析方法试一试：

img

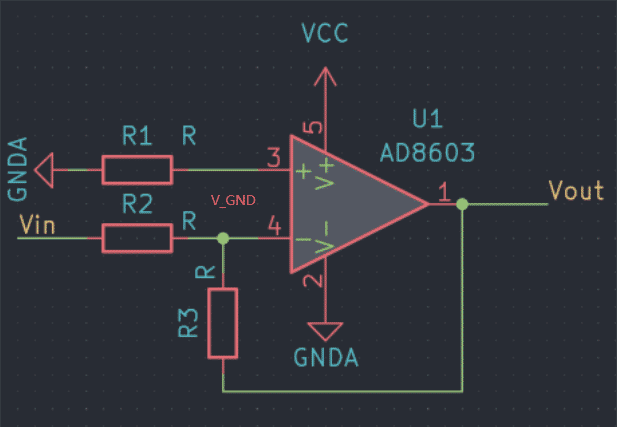
同样满足如下条件：

虚短：
$$
V_+ = V_- = V_{GND} = GNDA =0\
V_{GND}为V-和V+的值
$$
虚断：
$$
\frac{V_{in} - V_{GND}}{R_2}= \frac{V_{GND} - V_{out}}{R3}\
KCL方法推导电流相等、方向相反，以V_{GND}到V_{out}为正方向。
$$

化简得：
$$
V_{out} = -V_{in}\frac{R_3}{R_2}
$$
我们仿真一下，修改电路如下：

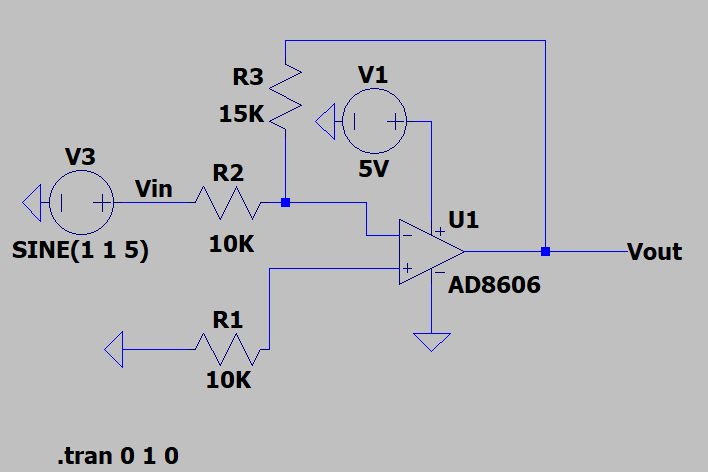
image-20220713232300943

对比上文的仿真，少了参考电压DC2V。

输出结果会是什么呢？

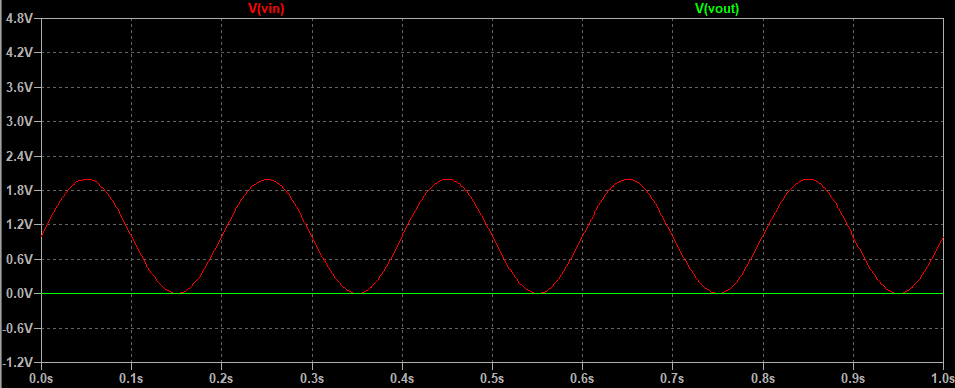
image-20220713232404566

为什么V_out没有波形呢？这里提示一下是放大器电源的问题，因为放大器此时没有负电压，我们再来修改一下，为放大器添加一个负电源：

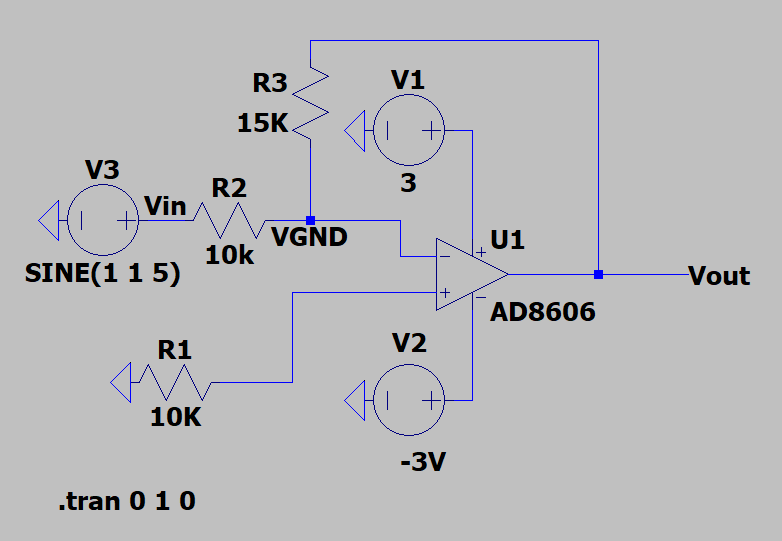
image-20220714123259531

因为AD8606的电源范围为0-6V，所以正负电源压差也不能超过6V，这里就是±3V。

仿真后效果如下：
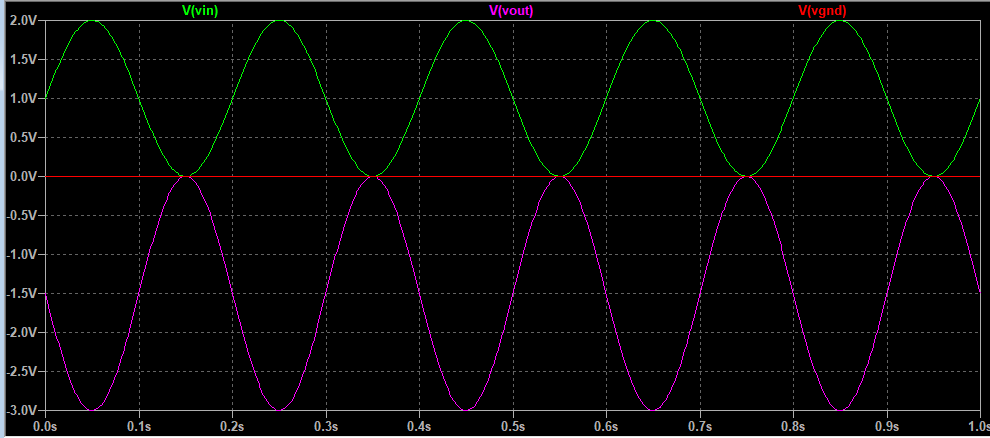
image-20220714123348596

存在三种情况：

  • $R3 > R2$ 反相放大
  • $R3 = R2$ 反相
  • $R3 < R2$ 反相缩小波形

电流放大\跨阻放大器

放大器常常还用于电流放大又叫跨阻放大器，结构更加简单，下面我先把电路举出来，然后解释一下原理：

下面是电路仿真截图:

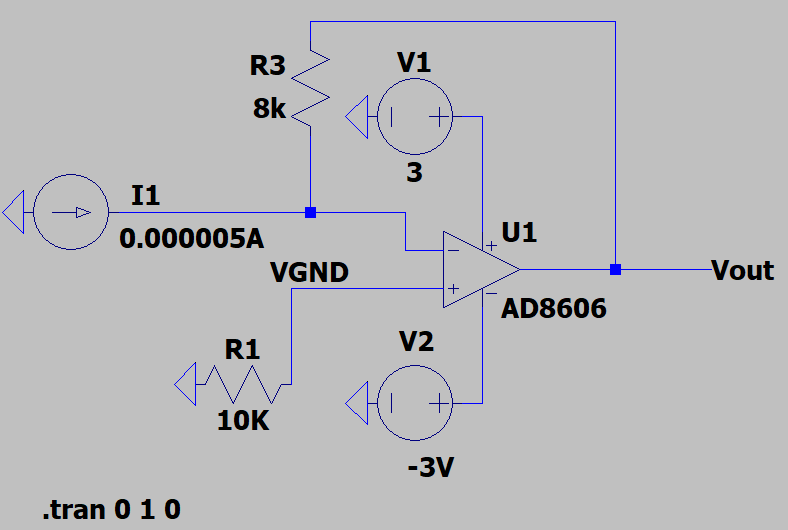
image-20220713235705056

我们将反向输入端换成了一个DC电流源,其提供的电流大小为$5\times10^{-6}A$.

下面我们来推导一下，它是如何放大的？

首先也是满足如下两种条件：

虚短：
$$
V_+ = V_- = V_{GND} \
V_{GND}为V-和V+的值
$$
虚断：
$$
I_1= \frac{V_{GND} - V_{out}}{R3}\
KCL方法推导电流相等、方向相反，以V_{GND}到V_{out}为正方向。
$$

因为$V_{GND}$是虚拟地电位为0,这里的虚拟地指的是其虚短条件，所以可以简化成如下:
$$
V_{out}=-R3 * I_1
$$
这时候我们就知道了，放大器输出的电压实际上是电流的倍数关系。需要注意的是这里的倍数关系还存在一个负值，输出的时候是一个负电压，仿真结果如下：

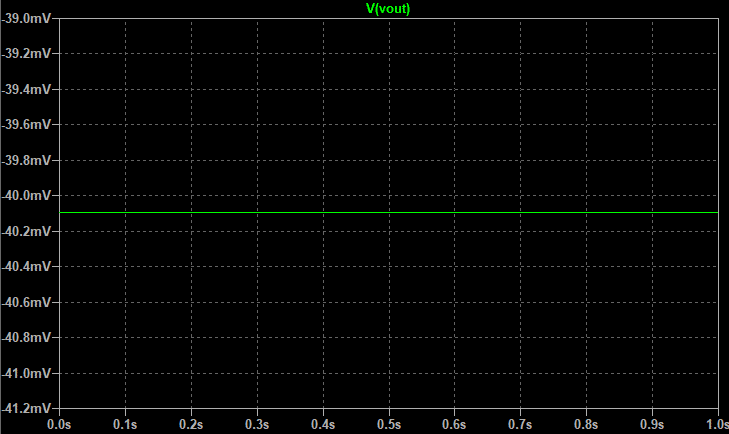
image-20220714123920761

你如果细心的话就会发现，实际上的值并不完全等于上述公式，为什么呢？我们分析的时候使用的是理想状态，实际上仿真的时候需要考虑偏置电压，详见上一篇运放参数。

完整的公式如下：
$$
I_1= \frac{V_{GND} +V_{offset}- V_{out}}{R3}\
$$
我们测量一下$V_{offset}$的值：

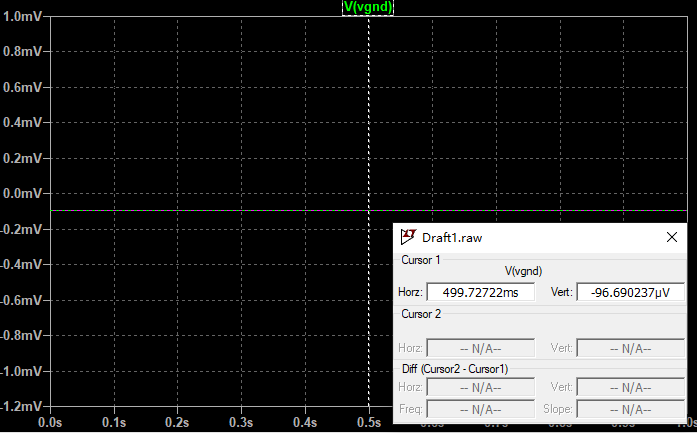
image-20220714134120857

用上边的公式计算一下：
$$
V_{out}= V_{offset}-I_1{R3} = -40.096(mv)\
$$
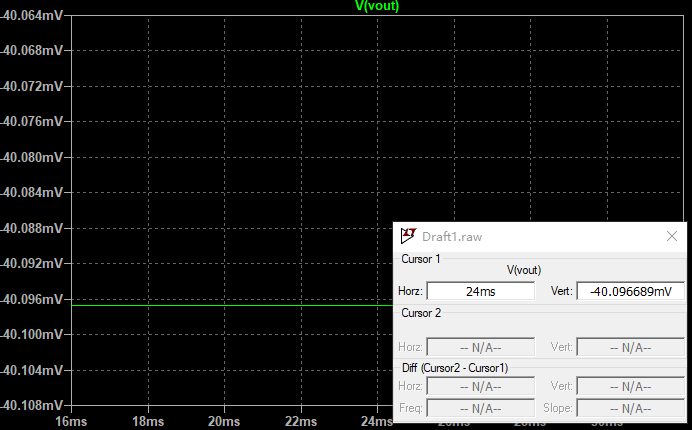
image-20220714134600871

我们再来增加一点难度：

image-20220714000647944

我们在+输入端增加一个电压，是不是很眼熟？这该如何推导呢？同样满足如下条件：

虚短：
$$
V_+ = V_- = V_{GND} \
V_{GND}为V-和V+的值
$$
虚断：
$$
I_1= \frac{V_{GND} - V_{out}}{R3}\
KCL方法推导电流相等、方向相反，以V_{GND}到V_{out}为正方向。
$$

此时$V_{GND}=1V$，我们再来推导一下：
$$
V_{out} = V_{GND} - I_1*R_3
$$
仿真结果如下：

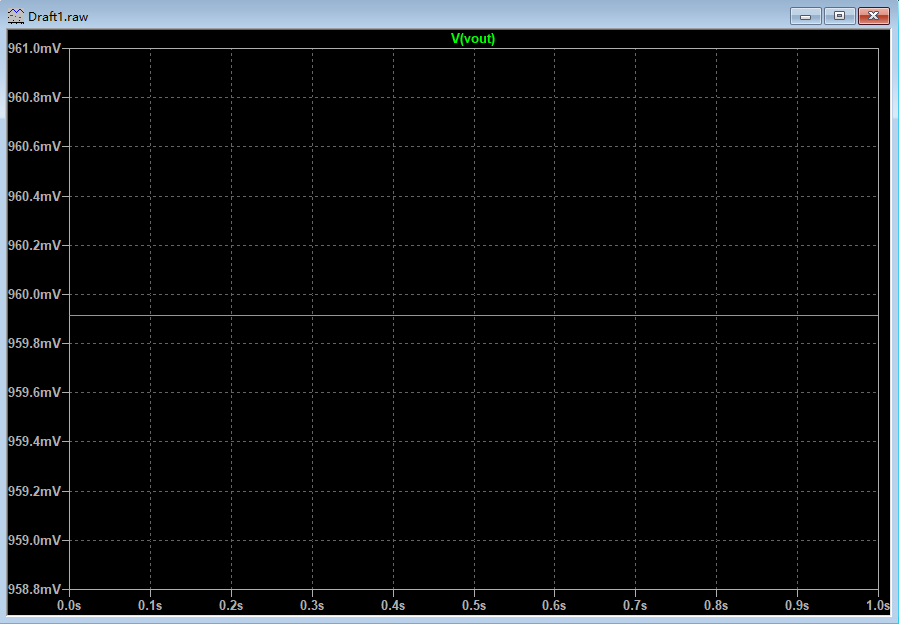
image-20220714001003426

反向加法电路

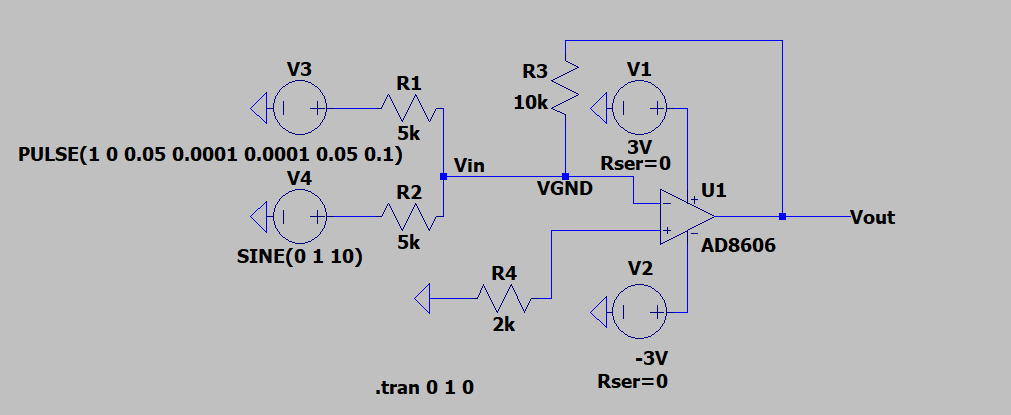
image-20220720182419709

其中信号$V_3$的参数如下：

Alt

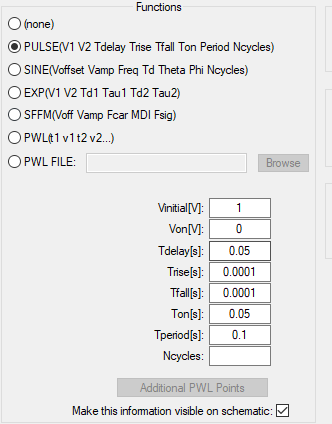
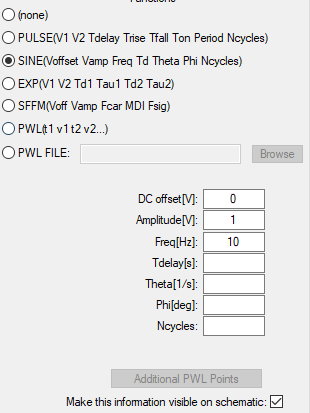
生成一个方波，周期位0.1s,上升下降波形较陡，持续时间为0.05s。

Alt

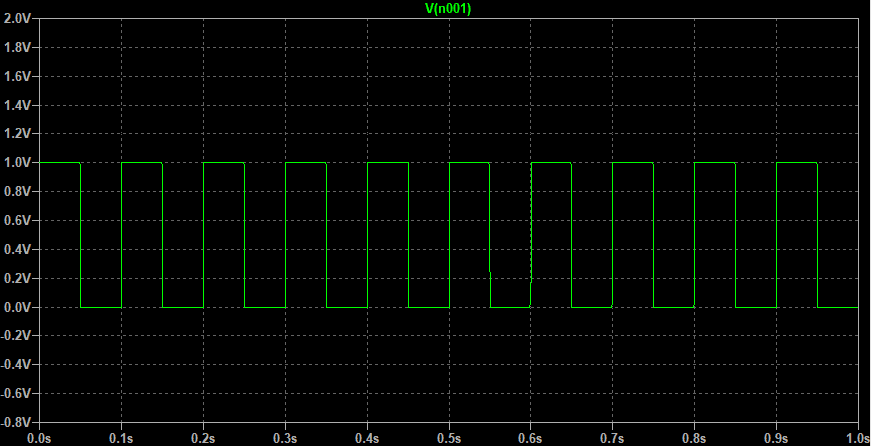
信号$V_4$正弦波形如下：

image-20220720182530450

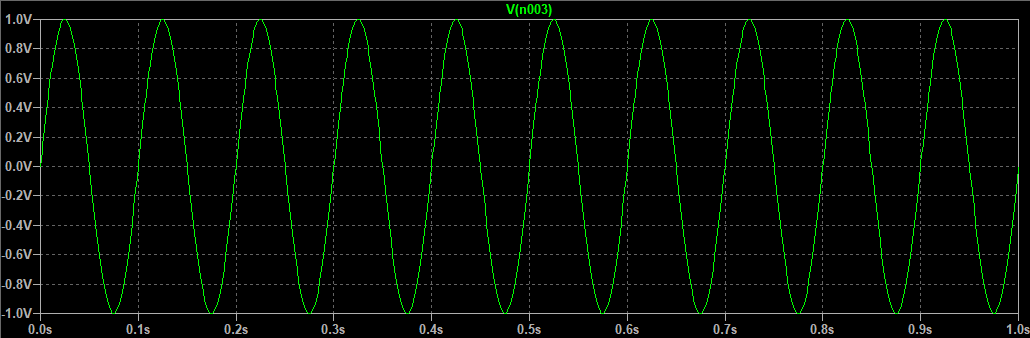
image-20220720182620369

推导过程如下：

同时也满足如下条件：

  • 虚短：

$$
Vin_+ = Vin_-
$$

  • 虚断：

$$
Iin_+ = Iin_- = 0
$$

则有：
$$
Vin_+ = Vin_- = 0\
I_{3} = I_{1}+I_{2}\电流跟随电阻序号
$$
对负数输入端使用KCL则有：
$$
\frac{V_{GND} - V_{out}}{R_3} = \frac{V_3 - V_{GND}}{R_1} + \frac{V_4 - V_{GND}}{R_2}
$$
化简得：
$$
V_{out} = - (\frac{R_3}{R_1}V_3 + \frac{R_3}{R_2}V_4 )
$$
实现了放大和相加，上图电路仿真结果如下：

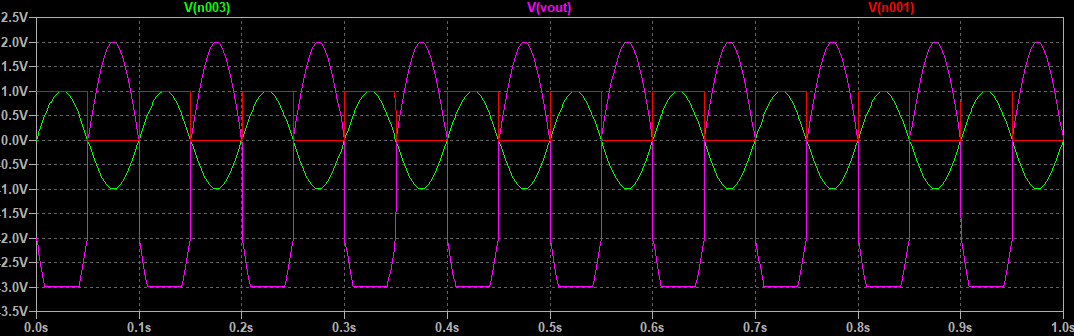
image-20220720183510646

思考问题

上文中正向输入端总是接一个10k的电阻的原因是什么？

其本质是平衡电阻，目的是为了减小运放输入偏置电流在电阻上形成的静态输入电压而带来误差(减少失调电压)。当运放的输入偏置电流较小，或信号较大，其影响可以忽略时，可以不用平衡电阻。某些并不需要平衡电阻。例如OPA227，其内部有校准好的电阻。

平衡电阻大小的推导过程

平衡电阻

image-20220714123259531

设输入电阻为$R2$，反馈电阻为$R3$，先假设同相端没有接平衡电阻，直接连接到地，设运放输入偏置电流为$IB$（同相端和反相端相同），流过$R2$和$R3$的电流分别为$I2$和$I3$，反相端电压为$V_-$，运放增益为$A$，那么在反相端运用$KCL$，有（设输入信号为0）：
$$
\frac{(0－V_-)}{R2}－\frac{(A - 1)V_-}{R3} ＝ I_B
$$
上式可得：
$$
V_- ＝ －\frac{(I_B × R2 × R3)}{R3＋(A - 1)R2}
$$
此时运放输出电压为：
$$
Vo＝A×\frac{(I_B×R2×R3)}{R3＋(A-1)R2}\
近似为：\
Vo＝I_B×((A*R2) // R3)\
注意这里是并联大小符号
$$
在不满足虚短的条件下，实际上$V_o$应该如何算呢？，需要注意的是这里不能直接使用虚短条件来运算，因为虚短的前提条件是忽略两端微小电压差。这里因为存在偏置电流所以不能省略。

如何计算，这里直接说结论，具体怎么来的请看专栏前文：
$$
V_o= A * V_{in}\
V_{in} = V_+ - V_-
$$
理论上如果是直接使用虚短条件，$V_o$大的大小应该等于零，但是经过上文分析，并不等于0，这是因为$V_{GND}$处电压不等于0，如果同相端通过一个电阻$R1$到地，且$R1＝R2//R3$，那么同相输入端电压为：
$$
V_＋＝I_B * R_1
$$
再对反相端分析（设输入信号为0）：
$$
\frac{(0－V_-)}{R_2} - \frac{( A ×(V_-)－(V_- - V_+))}{R_3}＝I_B
$$
上式子 $I_B = 0$,则此时放大器输出也等于0。

应用2

正向比例运算

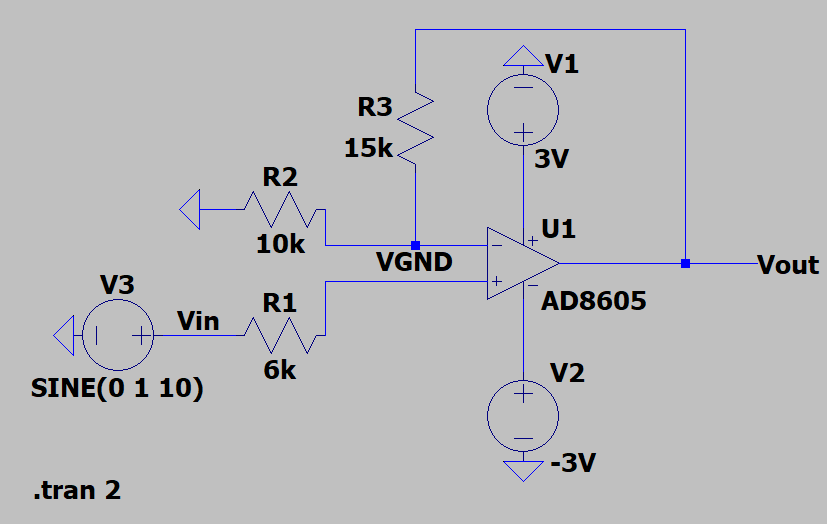
image-20220720174432642

同时也满足如下条件：

  • 虚短：

$$
Vin_+ = Vin_-
$$

  • 虚断：

$$
Iin_+ = Iin_- = 0
$$

此时VGND等于下边电压源所产生的电压，即满足下式：
$$
V_{GND}= V_+ = V_- = \sin{t}
$$
针对负输入端使用KCL可得：
$$
\frac{V_- - 0}{R_2}= \frac{V_{out} - V_{GND}}{R_3}
$$
化简得：
$$
V_+ \times (1+\frac{R_3}{R_2}) = V_{out}
$$
仿真结果如下：

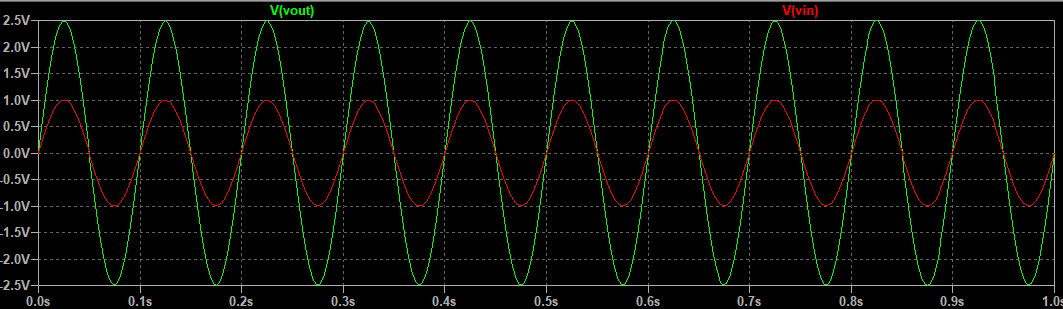
image-20220720174423802

同相比例输入电阻大，输出电阻小。需要注意的是有些运放对正向放大倍数有一定要求，所以推荐仔细观看手册。

电压跟随器

主要特点：输入阻抗高，输出阻抗低，常作为阻抗变换和缓冲级，提高输出能力。

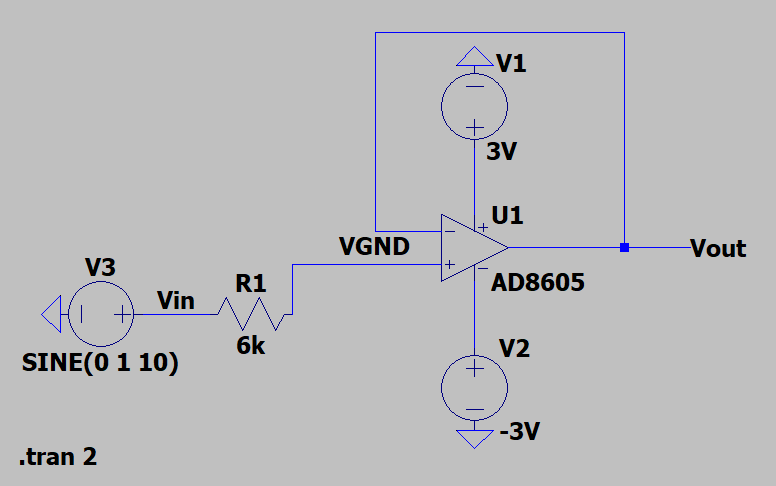
image-20220720175131290

其放大特点是不放大，没错就是输出电压和输入电压保持一致，具体推导实在过于简单，使用虚短即可。

一般的运放不能这样，只有数据手册寿命了，单位增益稳定（Unity-Gain Stable）的运放才可以:

image-20220720175614619

仿真结果：

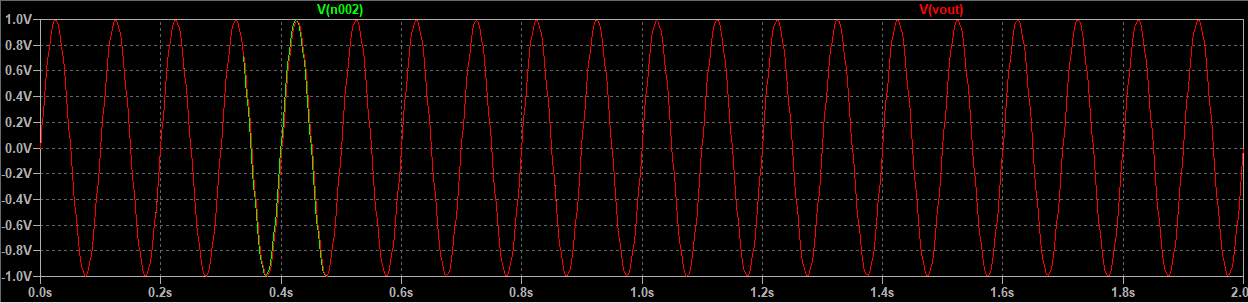
image-20220720175116800

同相加法器

通向加法器是使用最多的加法器，因为某些信号可能是含有负电压的，而单片机内置的ADC是无法采集负电压的，所以我们需要通过加法器辣酱对应的电压抬升，实现负电压采集。

举个例子，有以下电路：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9iBHL4zz-1658479233051)(https://s3.bmp.ovh/imgs/2022/07/20/37ac9ad8f071b78e.png)]

其中信号$V_3$的参数如下：

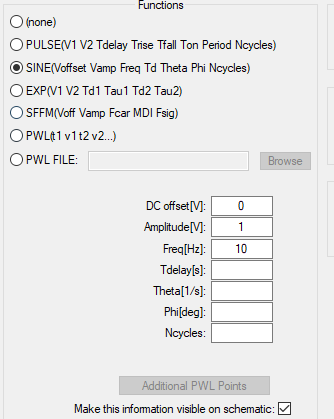
image-20220720184511182

波形如下：

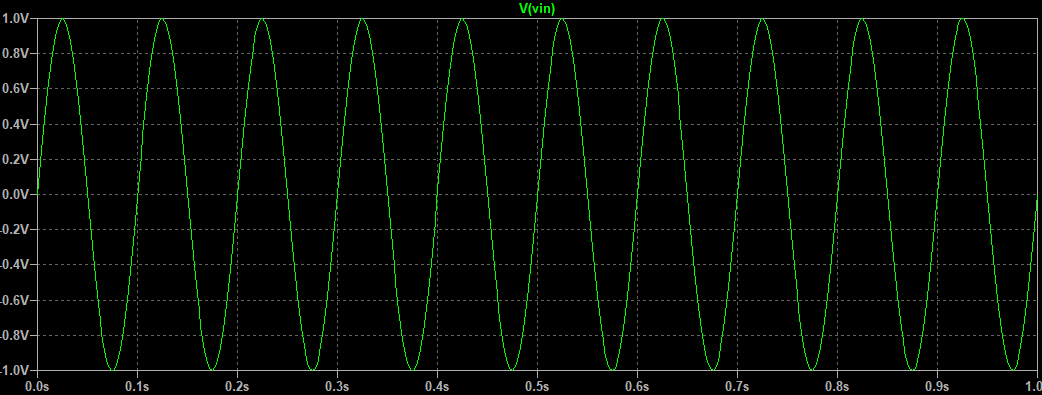
V4是一个DC1V的直流信号。

同时也满足如下条件：

  • 虚短：

$$
Vin_+ = Vin_-
$$

  • 虚断：

$$
Iin_+ = Iin_- = 0
$$

根据上式负输入端的分析则有：
$$
\frac{V_- - 0}{R2} =\frac{ V_{out} - V_-}{R_3}
$$
实际上我们对于$V_+$应该这样分析：

使用叠加定理。为了确定每个独立源的作用，所有的其他电源的必须“关闭”（置零）：

  1. 在所有其他独立电压源处用短路（Short circuit）代替（从而消除电压，即令V = 0；理想电压源的内部阻抗为零（短路））。
  2. 在所有其他独立电流源处用开路（Open circuit）代替 （从而消除电流，即令I = 0；理想的电流源的内部阻抗为无穷大（开路））。

依次对每个电源进行以上步骤，然后将所得的响应相加以确定电路的真实操作。所得到的电路操作是不同电压源和电流源的叠加。

我们知道$Iin_+ = Iin_- = 0$,那么就存在下式：
$$
V_+ = \frac{V_3 - 0}{R1+R_4} *R4 + \frac{V_4 - 0}{R1+R_4} *R1
$$
再根据虚短和对负输入端的分析则有：
$$
V_{out} = (1+\frac{R_3}{R_2})(\frac{V_3 }{R1+R_4} *R4 + \frac{V_4}{R1+R_4} *R1)
$$
当R1=R4=R3=R2的时候：

就满足：
$$
V_{out} =V_3+V_4
$$
仿真结果如下：

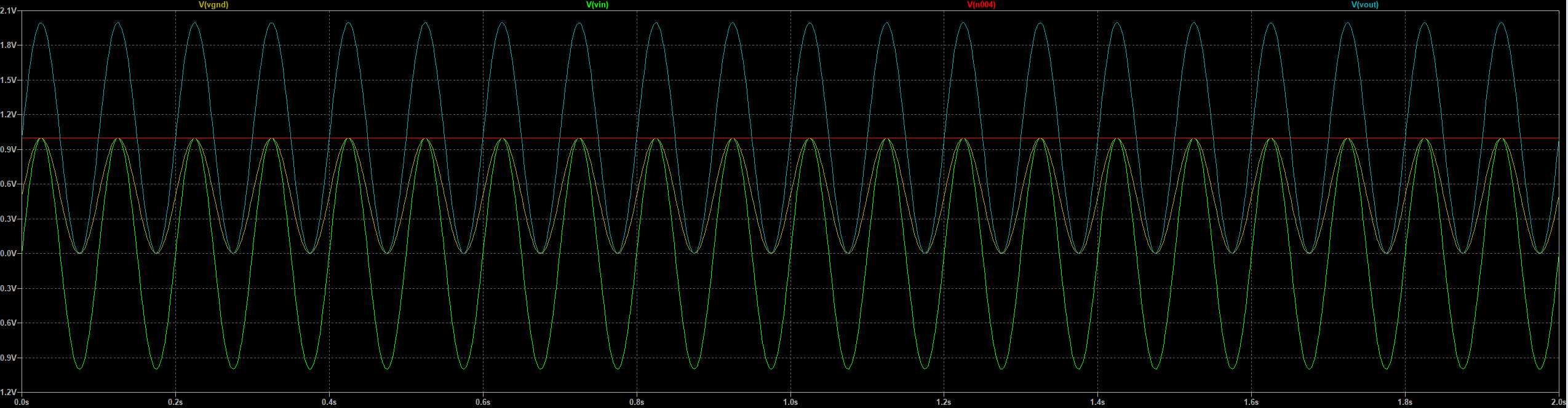
image-20220720193058452

其中V(gnd)为V+电压，V(n004)为V4信号，Vin和Vout如仿真中的标签。

减法运算电路

由于减法运算并不分正负所以我们把他单独列出来。

减法常常用于输出差分信号。

其电路一般如下：

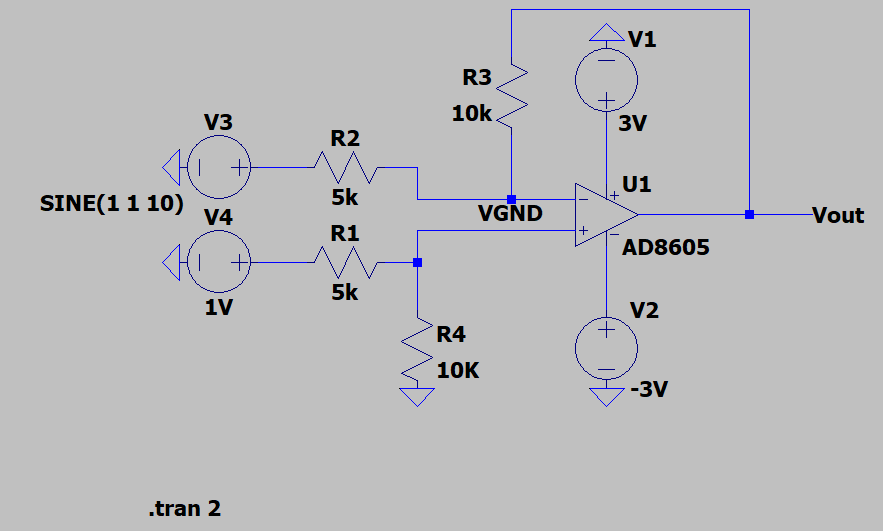
image-20220720194053859

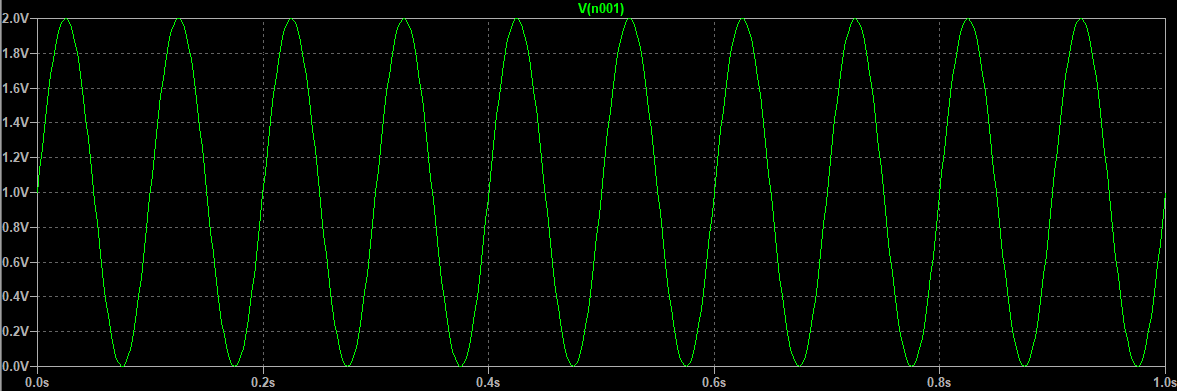
其中V_3为正弦波：
image-20220720194138888

V_4为直流电源1V。

同时也满足如下条件：

  • 虚短：

$$
Vin_+ = Vin_- = V_{GND}
$$

  • 虚断：

$$
Iin_+ = Iin_- = 0
$$

其中V_+的计算方法如下：
$$
V_+ = \frac{R_4}{R_1+R_4} * Vin_+
$$
其中对负输入端使用KCL分析如下：
$$
\frac{Vin_- V_{GND}}{R_2} = \frac{ V_{GND} - V_{out}}{R_3}
$$
将$Vin_+ = Vin_- = V_{GND}$带入得：
$$
V_{out} = Vin_+ \frac{R_4}{R_1+R_4}(1+\frac{R_3}{R_2}) - Vin_-(\frac{R_3}{R_2})
$$
当$R_3 = R_4且 R_1 =R_2$条件满足时

化简为：
$$
V_{out} = \frac{R_3}{R_2} ( Vin_+ - Vin_-)
$$
满足减法电路。

最后仿真结果如下：

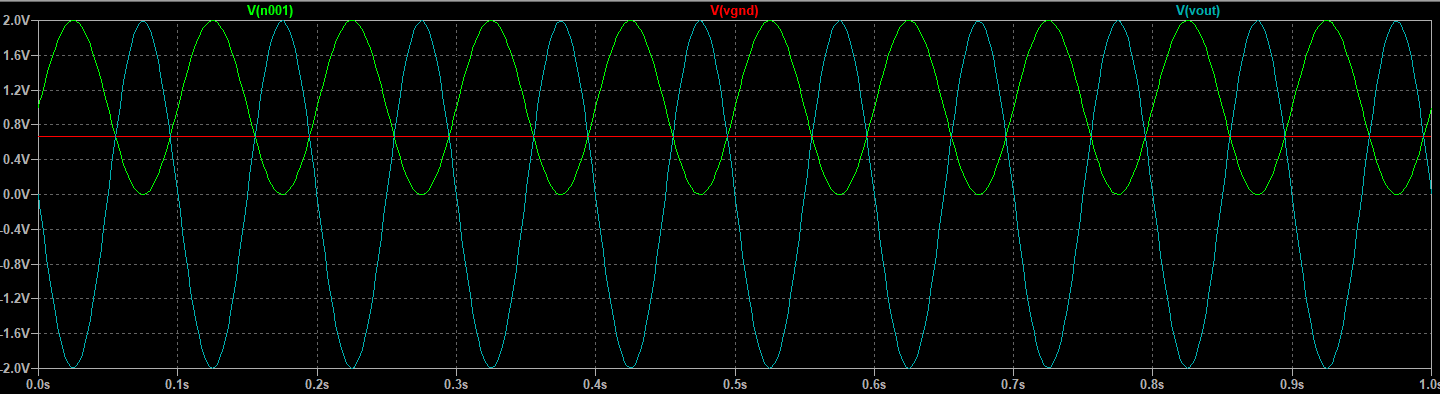
image-20220720200858123

其中V(gnd)为V+电压，V(n001)为V3信号，Vout如仿真中的标签。